Least Squares Line Of Best Fit Equation

A line of best fit can be roughly determined using an eyeball method by drawing a straight line on a scatter plot so that the number of points above the line and below the line is about equal and the line passes through as many points as possible.

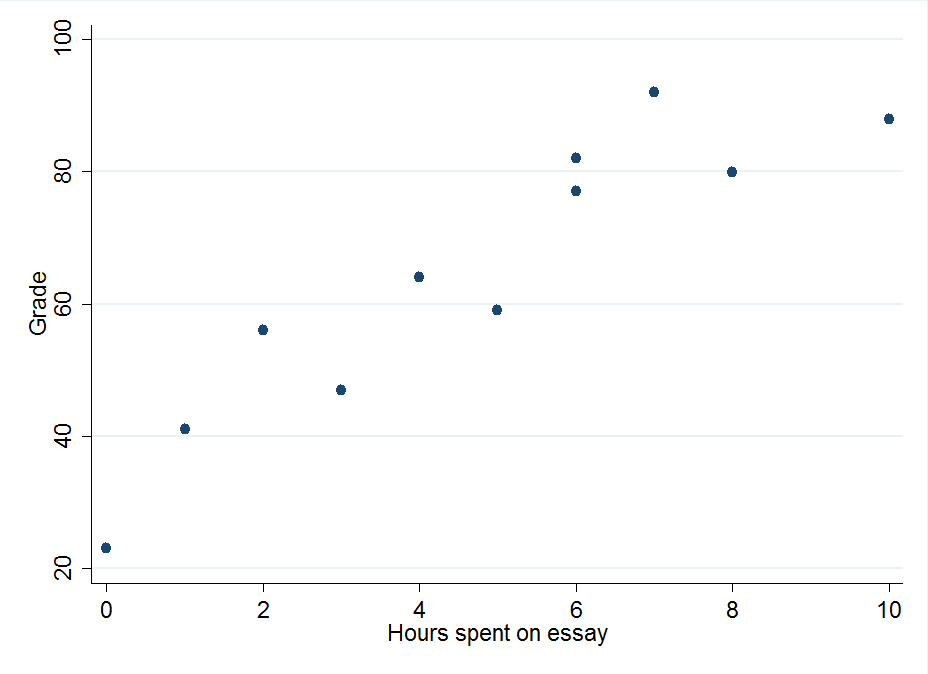
Least squares line of best fit equation. The method of least squares is a standard approach in regression analysis to approximate the solution of overdetermined systems sets of equations in which there are more equations than unknowns by minimizing the sum of the squares of the residuals made in the results of every single equation. Let us consider the following graph wherein a set of data is plotted along the x and y axis. These data points are represented using the blue dots. Line of best fit in the least square regression.

This is why the least squares line is also known as the line of best fit. Since the least squares line minimizes the squared distances between the line and our points we can think of this line as the one that best fits our data. Drawing a least squares regression line by hand. We can place the line by eye.

Least squares regression line of best fit. As we mentioned before this line should cross the means of both the time spent on the essay and the mean grade received. Imagine you have some points and want to have a line that best fits them like this. A more accurate way of finding the line of best fit is the least square method.

The line of best fit is a straight line drawn through a scatter of data points that best represents the relationship between them. If we wanted to draw a line of best fit we could calculate the estimated grade for a series of time values and then connect them with a ruler. Of all of the possible lines that could be drawn the least squares line is closest to the set of data as a whole. And there we have it.